சைன், கொசைன் மற்றும் டேன்ஜென்ட் ஆகியவை அன்றாட பள்ளி வாழ்க்கையில் பரவலாகப் பயன்படுத்தப்படுகின்றன, மேலும் அவற்றைப் பற்றி அறிந்திருப்பது அவசியம்
புரிந்து கொள்ள முக்கோணவியல்முக்கோணங்களின் கணிதப் படிப்பு, அப்பகுதியில் அதிக அறிவு உள்ள பெரியவர்களுக்கும் கூட பெரும் சவாலாக இருக்கும். கணக்கீடுகளும், சூத்திரங்களும் ‘எழுத்து சூப்’ போல் தோன்றினாலும், ஓரளவு முயற்சி செய்தால், பாடத்தைப் புரிந்துகொண்டு முன்னேற முடியும்.
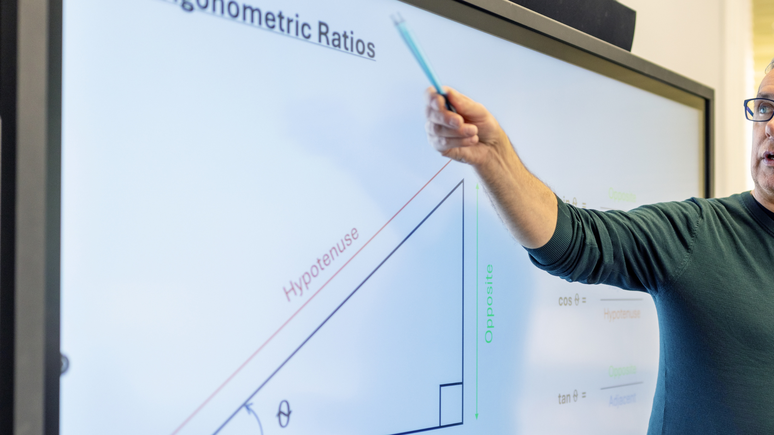
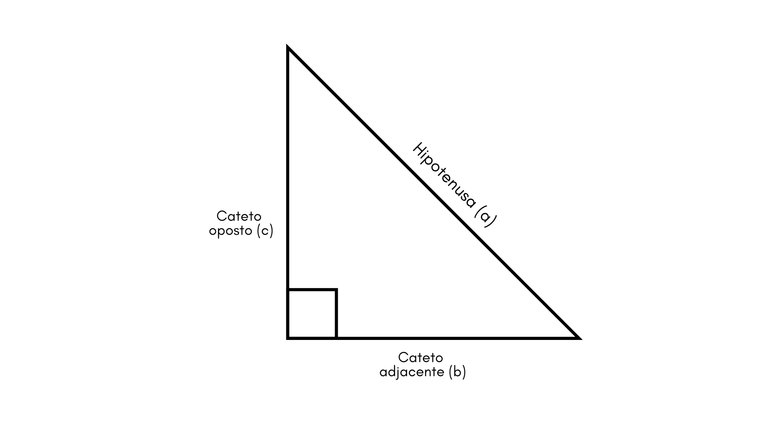
விஷயத்தைப் புரிந்து கொள்ள, நீங்கள் அடிப்படைகள் மற்றும் இந்த முழு அமைப்பு எவ்வாறு செயல்படுகிறது என்பதைப் புரிந்து கொள்ள வேண்டும். முக்கோணவியல் என்பது முக்கோணங்களின் கோணங்கள் மற்றும் பக்கங்களைக் கணக்கிடும் ஆய்வு ஆகும். தி வலது முக்கோணம் சமமான கோணத்துடன் மூன்று பக்கங்களால் உருவாகிறது 90º. அதில், ஒவ்வொரு பக்கமும் ஒரு பெயர் உள்ளது:
- ஹைபோடென்யூஸ் (அ): நீளமான பக்கம் மற்றும் வலது கோணத்தின் “முன்” ஒன்று.
- கேதீட்டஸ் (சி) எதிரே: பெயர் குறிப்பிடுவது போல, இது நீளமான பக்கத்திற்கு எதிரே உள்ளது.
- அருகிலுள்ள கேதீடஸ் (பி): ஒரு குறிப்பிட்ட கோணத்திற்கு அடுத்ததாக மற்றும் தீவிரத்தை உருவாக்குகிறது.
ஒன்றாக, அவை பித்தகோரியன் தேற்றத்தை உருவாக்குகின்றன: a2 = b2 + c2. எந்த முக்கோணத்தின் கோணங்களின் கூட்டுத்தொகை 180° ஆகும்.
பெரும்பாலான மக்கள் அடிப்படைக் கல்வியின் போது மட்டுமே முக்கோணவியலுடன் தொடர்பு கொண்டிருந்தாலும், பள்ளியில், இந்தக் கணக்கீடு தொழில் வல்லுநர்கள் மற்றும் நிறுவனங்களால் பரவலாகப் பயன்படுத்தப்படுகிறது. எடுத்துக்காட்டாக, அமெரிக்காவின் தேசிய ஏரோநாட்டிக்ஸ் மற்றும் ஸ்பேஸ் அட்மினிஸ்ட்ரேஷன் ஏஜென்சியான நாசா போர்ட்டலில், இந்த ஆய்வு விமானம் மற்றும் உந்துவிசை வளர்ச்சியில் பயன்படுத்தப்படுகிறது என்று விளக்கப்பட்டுள்ளது. இப்போது, நாம் அடுத்த கட்டத்திற்கு செல்லலாம்.
சைன், கொசைன் மற்றும் டேன்ஜென்ட்: அவை எதற்காக, எதற்காக?
சைன், கொசைன் மற்றும் டேன்ஜென்ட் ஆகியவை முக்கோணவியலின் மூன்று விகிதங்கள். அவை வலது கோண முக்கோணத்தின் பக்கங்களைக் கணக்கிடப் பயன்படுகின்றன, மேலும் கணக்கீடுகள் உருவாகும்போது, சூத்திரங்கள் உருவாக்கப்படுகின்றன.
சூத்திரங்கள்
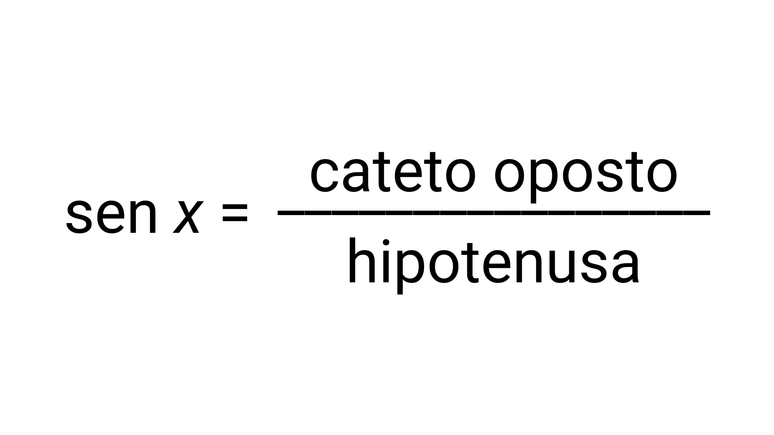
வலது முக்கோணத்தின் எதிர் பக்கத்திற்கும் ஹைப்போடென்யூஸுக்கும் இடையில் அடையாளம் காணப்பட்ட முதல் விகிதம் அழைக்கப்படுகிறது மார்பகம். அதற்கு சமமான சூத்திரம்: sin x = c / a.
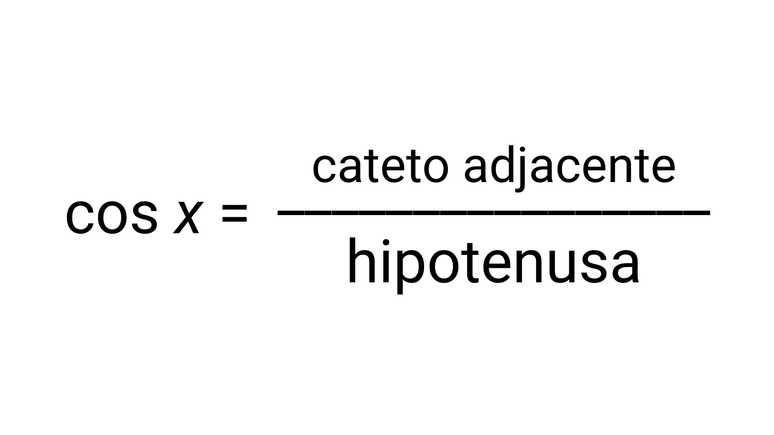
இரண்டாவது காரணம், அருகிலுள்ள பக்கத்திற்கும் ஹைபோடென்யூஸுக்கும் இடையில் அடையாளம் காணப்பட்டது, இது அழைக்கப்படுகிறது கொசைன். சூத்திரம் இதற்குச் சமமானது: cos x = b/a.
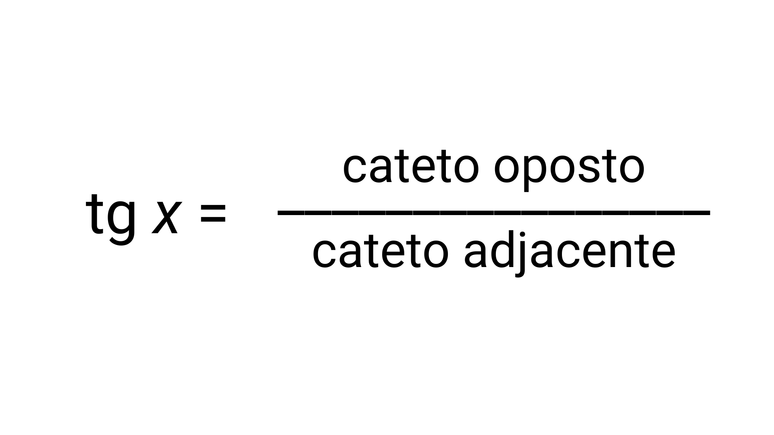
மூன்றாவது காரணம், எதிர் மற்றும் அருகில் உள்ள பக்கங்களுக்கு இடையில் அடையாளம் காணப்பட்டது தொடுகோடு. சூத்திரம் இதற்குச் சமமானது: tg x = c / b.